神经网络解常微分方程

解方程：
$$ \begin{cases}f’(x)=f(x) \\ f(0) = 1 \end{cases}$$

1
2
3
4
5
import torch
import torch.nn as nn
from torch.autograd import Function
from matplotlib import pyplot as plt
%matplotlib inline
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class NN(nn.Module):
    def __init__(self):
        super(NN, self).__init__()
        self.input_layer = nn.Linear(1, 20)
        self.hidden_layer = nn.ModuleList([nn.Linear(20, 20) for _ in range(4)])
        self.output_layer = nn.Linear(20, 1)
        self.act = nn.Tanh()

    def forward(self, x):
        o = self.act(self.input_layer(x))
        for _, hl in enumerate(self.hidden_layer):
            o = self.act(hl(o))
        out = self.output_layer(o)
        return out
1
x = torch.linspace(0, 2, 2000,requires_grad=True).unsqueeze(-1)
1
2
3
net = NN()
loss_fn = nn.MSELoss(reduction='mean')
optimizer = torch.optim.Adam(net.parameters(), lr=0.001)

$f(x)$在此是用神经网络NN进行逼近，则$f’(x)$是神经网络的输出对x的导数

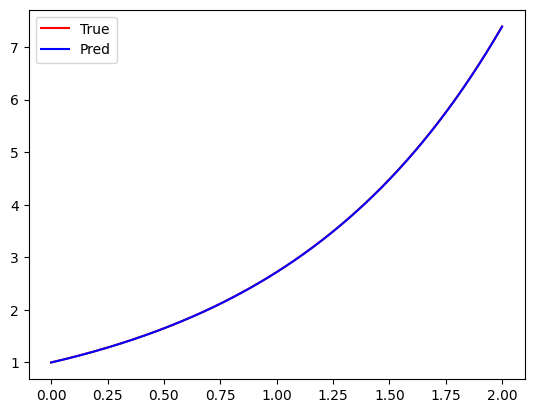
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
for epoch in range(1000):
    y_0 = net(torch.zeros(1))  # 初始条件

    f = net(x)  # f(x)
    pf, = torch.autograd.grad(f, 
                             x, 
                             grad_outputs=torch.ones_like(net(x)), 
                             create_graph=True)  # f'(x)

    optimizer.zero_grad()

    Mse1 = loss_fn(f, pf)
    Mse2 = loss_fn(y_0, torch.ones(1))  # ?
    loss = Mse1 + Mse2

    loss.backward()
    optimizer.step()
    if epoch % 200 == 0:
        print("epoch:{}, loss:{}".format(epoch, loss.item()))

y = torch.exp(x)

y1 = net(x)
plt.plot(x.detach().numpy(), y.detach().numpy(), c='red', label='True')
plt.plot(x.detach().numpy(), y1.detach().numpy(), c='blue', label='Pred')
plt.legend(loc='best')

plt.show()
epoch:0, loss:1.452800989151001
epoch:200, loss:0.09077981114387512
epoch:400, loss:0.0009344415157102048
epoch:600, loss:0.0003904764889739454
epoch:800, loss:0.0001252157671842724

png