神经网络解偏微分方程

1
%reset -f
1
2
3
import torch.nn as nn
import torch
from torch.autograd import Function
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class NN(nn.Module):
    def __init__(self):
        # NL是有多少层隐藏层
        # NN是每层的神经元数量
        super(NN, self).__init__()
        self.input_layer = nn.Linear(2, 20)
        self.hidden_layer = nn.ModuleList([nn.Linear(20, 20) for _ in range(4)])
        self.output_layer = nn.Linear(20, 1)
        self.act = nn.Tanh()
 
    def forward(self, x):
        o = self.act(self.input_layer(x))
        for _, hl in enumerate(self.hidden_layer):
            o = self.act(hl(o))
        out = self.output_layer(o)
        return out

\begin{cases}u_t+uu_x-(0.01/\pi)u_{xx}=0,x\in[-1,1],t\in[0,1]\\ u(0,x)=-sin(\pi x),\\ u(t,-1)=u(t,1)=0\end{cases}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def sample(size):
    # x = torch.cat((torch.rand([size, 1]), torch.full([size, 1], -1) + torch.rand([size, 1]) * 2), dim=1)
    # x[:,0]: t (0~1)随机分布值;  x[,:1]: x (-1~1)随机分布值

    # 因为后面有sin(πx),所以这里得先把x存下来，并且保证和带入初值的x_initial(t,x)的x部分是相同的
    # x_init = torch.full([size, 1], -1) + torch.rand([size, 1]) * 2
    
    # x_init: (-1~1)随机分布值

    # x_initial = torch.cat((torch.zeros(size, 1), x_init), dim=1)
    # x_initial[:,0]: t 0; x_initial[:,1]: x == x_init: (-1~1)随机分布值

    # x_boundary_left = torch.cat((torch.rand([size, 1]), torch.full([size, 1], -1)), dim=1)
    # x_boundary_left[:,0]: t (0~1)随机分布值;  x_boundary_left[:,1]: x -1

    # x_boundary_right = torch.cat((torch.rand([size, 1]), torch.ones([size, 1])), dim=1)
    # x_boundary_left[:,0]: t (0~1)随机分布值;  x_boundary_left[:,1]: x 1

    x = torch.cat((torch.rand([size, 1]) * 0.4, torch.rand([size, 1]) * 2), dim=1)
    x_init = torch.rand([size, 1]) * 2
    x_initial = torch.cat((torch.zeros(size, 1), x_init), dim=1)
    x_boundary_left = torch.cat((torch.rand([size, 1]) * 0.4, torch.zeros([size, 1])), dim=1)
    x_boundary_right = torch.cat((torch.rand([size, 1]) * 0.4, torch.full([size, 1], 2)), dim=1)

    return x, x_initial, x_init, x_boundary_left, x_boundary_right
1
2
3
4
5
size = 2000
x_train, x_initial, x_init, x_left, x_right = sample(size)
net = NN()
optimizer = torch.optim.Adam(net.parameters(), lr=1e-3)
lossf = nn.MSELoss(reduction='mean')

\begin{cases}u_t+uu_x-(0.01/\pi)u_{xx}=0,x\in[-1,1],t\in[0,1]\\ u(0,x)=-sin(\pi x),\\ u(t,-1)=u(t,1)=0\end{cases}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
for epoch in range(10000):
    x = torch.autograd.Variable(x_train, requires_grad=True)
    d = torch.autograd.grad(net(x), x, grad_outputs=torch.ones_like(net(x)), create_graph=True)
    dt = d[0][:, 0].unsqueeze(-1)
    dx = d[0][:, 1].unsqueeze(-1)
    dxx = torch.autograd.grad(dx, x, grad_outputs=torch.ones_like(dx), create_graph=True)[0][:, 1].unsqueeze(-1)

    optimizer.zero_grad()

    y_train = net(x)

    # loss1 = lossf(dt + y_train * dx, (0.01 / torch.pi) * dxx)
    loss1 = lossf(dt + y_train * dx, (0.01) * dxx)
    # loss2 = lossf(net(x_initial), -1 * torch.sin(torch.pi * x_init))
    loss2 = lossf(net(x_initial), torch.sin(torch.pi * x_init))
    loss3 = lossf(net(x_left), torch.zeros([size, 1]))
    loss4 = lossf(net(x_right), torch.zeros([size, 1]))
    
    loss = loss1 + loss2 + loss3 + loss4
    
    loss.backward()
    optimizer.step()

    if epoch % 100 == 0:
            print(f'step: {epoch}  loss = {loss.item()}')
step: 0  loss = 0.5008491277694702
step: 100  loss = 0.42394745349884033
step: 200  loss = 0.16642776131629944
...
step: 9700  loss = 0.00022392613755073398
step: 9800  loss = 0.002956720534712076
step: 9900  loss = 0.00017632679373491555

1
2
x_test = torch.cat((torch.full([size, 1], 0.4), torch.linspace(0,2,2000).unsqueeze(-1)), dim=1)
y_test = net(x_test)
1
2
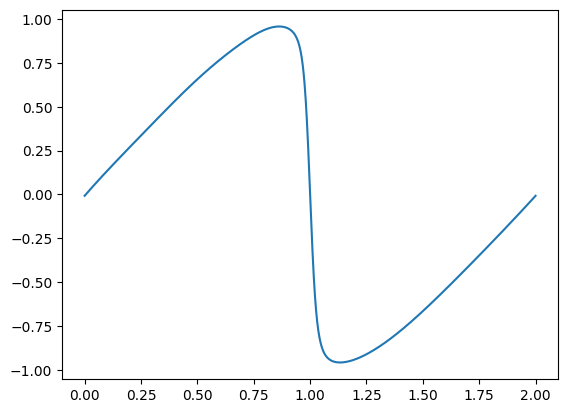
from matplotlib import pyplot as plt
plt.plot(torch.linspace(0,2,2000).numpy(), y_test[:,0].detach().numpy())
[<matplotlib.lines.Line2D at 0x215ff55b1c0>]

png