1
%reset -f

四阶RK法：
首先将方程转化为标准形式：
$$\begin{cases}\dot{\mathrm{y_1}}&=\mathrm{f_1}\left(\mathrm{y_1},\cdots,\mathrm{y_n},\mathrm{t}\right)\\ &\vdots\\ \dot{\mathrm{y_n}}&=\mathrm{f_n}\left(\mathrm{y_1},\cdots,\mathrm{y_n},\mathrm{t}\right)\end{cases}$$

$$\begin{cases}
h_m =& t_{m+1} - t_m \\
k_{1i}^m =& f_i(y_1^m, \cdots, y_i^m, \cdots, y_n^m, t_m) \\
k_{2i}^m =& f_i(y_1^m, \cdots, y_i^m + \frac{h_m}{2}k_{1i}^m, \cdots, y_n^m, t_m + \frac{h_m}{2}) \\
k_{3i}^m =& f_i(y_1^m, \cdots, y_i^m + \frac{h_m}{2}k_{2i}^m, \cdots, y_n^m, t_m + \frac{h_m}{2}) \\
k_{4i}^m =& f_i(y_1^m, \cdots, y_i^m + h_m k_{3i}^m, \cdots, y_n^m, t_m + \frac{h_m}{2}) \\
y_i^{m+1} =& y_i^m + \frac{h_m}{6}(k_{1i}^m + 2k_{2i}^m + 2k_{3i}^m + k_{4i}^m)
\end{cases}$$

例，解如下：
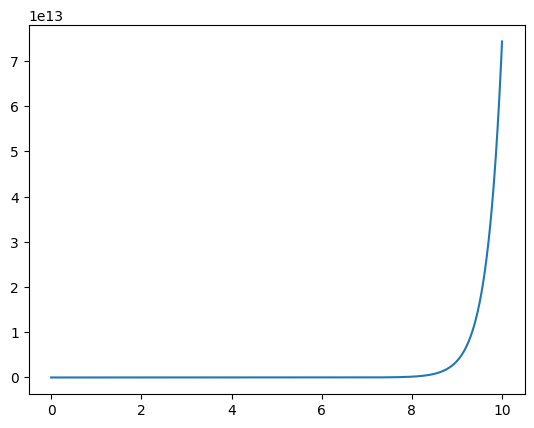
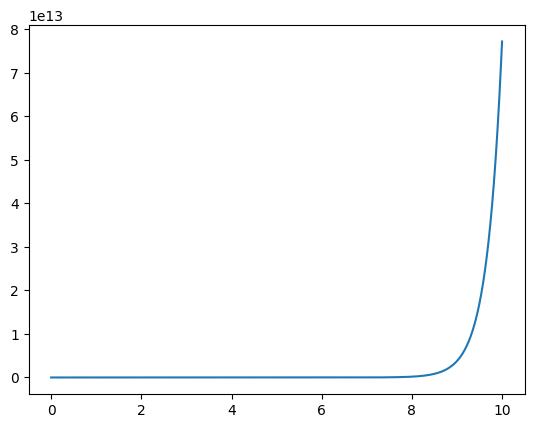
$$\begin{aligned}&\cfrac{dx}{dt}=x+2y\\ &\cfrac{dy}{dt}=3x+2y,\end{aligned}\qquad\begin{cases}x(0)=6\\ y(0)=4\end{cases}$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import numpy as np
nt = 500
tlim = [0., 10.]
t = np.linspace(tlim[0], tlim[1], nt)

x = np.zeros_like(t)
y = np.zeros_like(t)

x[0] = 6.
y[0] = 4.

def f1(x, y):
    return x + 2*y

def f2(x, y):
    return 3*x + 2*y

$$\begin{cases}\dot{\mathrm{y_1}}&=\mathrm{f_1}\left(\mathrm{y_1},\cdots,\mathrm{y_n},\mathrm{t}\right)\\ &\vdots\\ \dot{\mathrm{y_n}}&=\mathrm{f_n}\left(\mathrm{y_1},\cdots,\mathrm{y_n},\mathrm{t}\right)\end{cases}$$

$$\begin{cases}
h_m =& t_{m+1} - t_m \\
k_{1i}^m =& f_i(y_1^m, \cdots, y_i^m, \cdots, y_n^m, t_m) \\
k_{2i}^m =& f_i(y_1^m, \cdots, y_i^m + \frac{h_m}{2}k_{1i}^m, \cdots, y_n^m, t_m + \frac{h_m}{2}) \\
k_{3i}^m =& f_i(y_1^m, \cdots, y_i^m + \frac{h_m}{2}k_{2i}^m, \cdots, y_n^m, t_m + \frac{h_m}{2}) \\
k_{4i}^m =& f_i(y_1^m, \cdots, y_i^m + h_m k_{3i}^m, \cdots, y_n^m, t_m + \frac{h_m}{2}) \\
y_i^{m+1} =& y_i^m + \frac{h_m}{6}(k_{1i}^m + 2k_{2i}^m + 2k_{3i}^m + k_{4i}^m)
\end{cases}$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
for m in range(nt-1):
    h_m = t[m+1] - t[m]

    k_m_1x = f1(x[m], y[m])
    k_m_1y = f2(x[m], y[m])

    k_m_2x = f1(x[m] + (h_m/2 * k_m_1x), y[m])
    k_m_2y = f2(x[m], y[m] + (h_m/2 * k_m_1y))

    k_m_3x = f1(x[m] + (h_m/2 * k_m_2x), y[m])
    k_m_3y = f2(x[m], y[m] + (h_m/2 * k_m_2y))

    k_m_4x = f1(x[m] + (h_m * k_m_3x), y[m])
    k_m_4y = f2(x[m], y[m] + (h_m * k_m_3y))

    x[m+1] = x[m] + h_m / 6. * (k_m_1x + 2*k_m_2x + 2*k_m_3x + k_m_4x)
    y[m+1] = x[m] + h_m / 6. * (k_m_1y + 2*k_m_2y + 2*k_m_3y + k_m_4y)
1
2
3
4
from matplotlib import pyplot as plt 
plt.plot(t, x)
plt.figure()
plt.plot(t, y)
[<matplotlib.lines.Line2D at 0x2448def2d90>]

png

png